Find the reciprocal

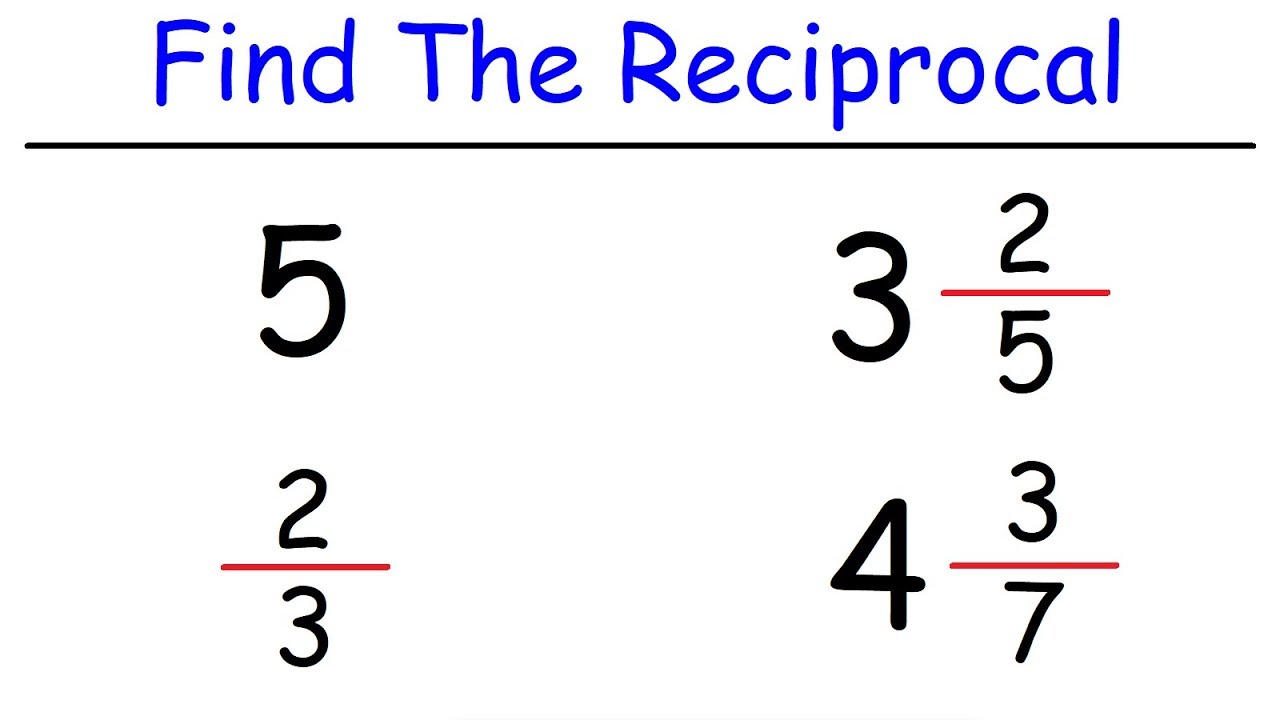
To find the reciprocal of a number, simply divide 1 by that number. For example, the reciprocal of 4 is 1/4, and the reciprocal of 0.5 is 2. This straightforward calculation allows you to quickly identify the multiplicative inverse of any non-zero number.

For negative numbers, the same rule applies. The reciprocal of -3 is -1/3. Keep in mind that the only number without a reciprocal is zero, since division by zero is undefined. When working with fractions, take the reciprocal by flipping the numerator and denominator; for instance, the reciprocal of 3/5 is 5/3.

This concept plays a significant role in various mathematical operations, including solving equations and understanding proportions. Use reciprocals to simplify complex calculations and verify your work through multiplication. With practice, finding reciprocals becomes an easy and efficient task.

Find the Reciprocal: A Practical Guide

To find the reciprocal of a number, simply divide 1 by that number. For example:

• Reciprocal of 2: 1 ÷ 2 = 0.5
• Reciprocal of 5: 1 ÷ 5 = 0.2
• Reciprocal of 0.25: 1 ÷ 0.25 = 4

If the number is a fraction, invert the fraction. For instance:

• Reciprocal of 3/4: Invert to 4/3
• Reciprocal of 7/2: Invert to 2/7

Handling negative numbers? The reciprocal remains negative. Examples include:

• Reciprocal of -3: 1 ÷ -3 = -0.333
• Reciprocal of -1/4: Invert to -4

Finding the reciprocal of zero isn’t possible, as division by zero is undefined. Keep this in mind to avoid errors in calculations.

Practicing with various numbers solidifies understanding. Try these for practice:

1. Find the reciprocal of 8.
2. Find the reciprocal of -2/3.
3. Find the reciprocal of 0.1.

Verify your results with the multiplication property: a number multiplied by its reciprocal equals 1. For example:

• 2 × 0.5 = 1
• 3/4 × 4/3 = 1

Use these steps and tips to confidently determine reciprocals in calculations and problem-solving tasks. Consistent practice will lead to quick identification of reciprocals without hesitation.

Understanding the Concept of Reciprocal

The reciprocal of a number is its multiplicative inverse. For any non-zero number x, the reciprocal is defined as 1/x. This means that when you multiply a number by its reciprocal, the result is always 1. For instance, the reciprocal of 2 is 1/2 and vice versa, 2 * (1/2) = 1.

Calculating Reciprocals

To find the reciprocal of a fraction, simply flip its numerator and denominator. For example, the reciprocal of 3/4 becomes 4/3. If dealing with mixed numbers, convert them to improper fractions first. For instance, 2 1/2 converts to 5/2, making its reciprocal 2/5.

Applications of Reciprocals

Reciprocals play a significant role in various mathematical operations, especially in division. Dividing by a number is equivalent to multiplying by its reciprocal. For example, dividing by 4 means multiplying by 1/4. In algebra, understanding reciprocals aids in solving equations and simplifying expressions.

Familiarize yourself with the properties of reciprocals to enhance your problem-solving skills. Recognize that the reciprocal of zero is undefined, as division by zero is not permissible. Being comfortable with this concept will boost your confidence in performing calculations and understanding mathematical relationships.

How to Calculate the Reciprocal of a Number

To find the reciprocal of a number, simply divide 1 by that number. For example, the reciprocal of 5 is 1 divided by 5, which equals 0.2. If you have a fraction, such as 3/4, the reciprocal is obtained by flipping the fraction, resulting in 4/3.

Steps to Calculate the Reciprocal

1. Identify the number for which you want the reciprocal.

2. If it’s a whole number (like 7), calculate 1 divided by that number (1/7 = 0.142857).

3. For fractions, invert the fraction. The reciprocal of a fraction a/b is b/a.

Special Cases

The reciprocal of 0 is undefined because you cannot divide by zero. For negative numbers, the process remains the same; for instance, the reciprocal of -2 is -0.5. Always remember that the reciprocal changes the sign if the number is negative.

Reciprocal of Fractions: Step-by-Step Process

To find the reciprocal of a fraction, simply follow this straightforward method: take the given fraction and flip its numerator and denominator.

For example, if the fraction is 3/4, the reciprocal becomes 4/3. This rule applies to any fraction, including improper fractions. For an improper fraction, such as 5/2, its reciprocal is 2/5.

In case your fraction is a whole number, remember to express it as a fraction over one. For instance, the whole number 6 can be written as 6/1, making its reciprocal 1/6.

For fractions with a zero in the numerator, such as 0/7, the reciprocal is undefined. Since division by zero is not possible, it’s crucial to recognize this limitation.

Every reciprocal has a relationship with its original fraction; multiplying a fraction by its reciprocal yields 1. For example, 3/4 multiplied by 4/3 equals 12/12, which simplifies to 1.

Practice makes perfect. Converting fractions into their reciprocals will become second nature as you apply this method consistently.

Determining the Reciprocal of Negative Numbers

The reciprocal of a negative number is simply the negative of its reciprocal value. For any negative number, say -x, the reciprocal is calculated as -1/x. This means that if you have a number like -4, its reciprocal would be -1/4, which equals -0.25.

Understanding this concept helps in various mathematical applications, such as solving equations or simplifying fractions. For example, if you multiply -4 by its reciprocal -1/4, the result will be -1. This property holds true for all negative numbers, reinforcing the idea that the product of a number and its reciprocal always equals -1 for negatives.

Keep in mind that the reciprocal of zero is undefined, so ensure your calculations exclude it. When working with negative fractions, the same rule applies. For instance, the reciprocal of -3/2 is -2/3. Simplifying the process comes down to flipping the numerator and denominator and retaining the negative sign.

This principle can also aid in understanding complex expressions. If you encounter a negative fraction or integer in an equation, simply apply the same steps to find its reciprocal efficiently. By maintaining clarity in your calculations, you’ll enhance your problem-solving skills.

In summary, calculating the reciprocal of negative numbers follows a straightforward pattern. Just remember to keep the negative sign while flipping the fraction or number. With practice, this method becomes second nature.

Reciprocals in Decimal Form: Conversion Techniques

To convert a fraction to its decimal reciprocal, simply divide 1 by the fraction. For instance, the reciprocal of 1/4 is obtained by calculating 1 ÷ (1/4), which equals 4. This technique applies to any fractional input, making it straightforward to determine recirpocal values.

Repeating Decimals

Some fractions produce repeating decimals. For example, 1/3 equals 0.333… This notation indicates a recurring sequence. To find its reciprocal, calculate 1 ÷ (1/3), leading to 3. When encountering a repeating decimal, aim to express the fraction accurately to achieve a precise reciprocal.

Using Long Division

Long division can be useful for obtaining the decimal form of a fraction. For example, to convert 2/5 into decimal form, perform long division. Dividing 2 by 5 gives 0.4. The reciprocal in decimal form becomes 1 ÷ 0.4, simplifying to 2. Mastering long division strengthens conversion skills and enhances accuracy.

Common Mistakes When Finding Reciprocals

One frequent mistake occurs when individuals attempt to find the reciprocal of zero. Recall that the reciprocal is defined as 1 divided by the number, and since division by zero is undefined, this operation cannot be performed.

Another common error is neglecting to check if a fraction is in its simplest form before finding its reciprocal. For example, the reciprocal of 2/4 is often mistakenly calculated as 4/2 instead of simplifying it first to 1/2. Thus, the correct reciprocal is 2.

Misunderstanding Positive and Negative Numbers

It’s crucial to maintain the sign of the original number when finding its reciprocal. For instance, the reciprocal of -3 is -1/3, yet many forget to include the negative sign, inadvertently writing it as 1/3. Always ensure the sign is accurate.

Confusing Whole Numbers and Fractions

Some struggle to convert whole numbers into fractions before finding their reciprocals. A whole number like 5 should be treated as 5/1. The reciprocal is then 1/5. Missing this conversion can lead to incorrect answers.

Value	Reciprocal
0	Undefined
2/4	2
-3	-1/3
5	1/5

Final advice: always double-check calculations to avoid these pitfalls. Understanding these common mistakes will significantly improve accuracy when finding reciprocals.

Applications of Reciprocals in Real Life Scenarios

Utilize reciprocals to enhance various aspects of daily life, from finance to nutrition. Understanding how to calculate reciprocals can streamline decision-making processes.

• Finance: Apply reciprocals when evaluating investments. For example, a return on investment (ROI) of 20% can be expressed as a reciprocal of 5 (1/0.20). This simplifies comparisons between various investment opportunities.

• Health and Fitness: Use reciprocals to calculate optimal workout intensity. If a training program calls for a 60% intensity, use the reciprocal (1/0.60) to determine rest times or recovery rates between sets.

• Cooking and Recipes: Adjust recipes by converting ingredient ratios. For a recipe that requires 2 cups of flour for 4 servings, find the reciprocal to scale it for 1 serving by dividing 2 by 4, leading to 0.5 cups.

• Construction: Calculate material requirements efficiently. If a plan dictates that 1 square foot of material covers an area of 8 square feet, apply the reciprocal (1/8) to estimate total material needed for larger projects.

• Education: Help students grasp concepts in advanced mathematics. Use reciprocals to simplify fractions, making it easier for learners to solve equations and compare ratios.

Recognizing and using reciprocals can significantly improve practical applications across various sectors, saving time and enhancing productivity.

Using Reciprocals in Algebraic Expressions

Apply reciprocals in algebraic expressions to simplify calculations and solve equations efficiently. In cases involving division, replace the divisor by its reciprocal to transform the expression. For instance, dividing by \( \frac{1}{a} \) can be expressed as multiplying by \( a \).

Multiplication and Division

When you encounter a situation like \( \frac{3}{4} \div \frac{2}{5} \), you can rewrite it as \( \frac{3}{4} \times \frac{5}{2} \). This approach streamlines the process, allowing you to multiply across the numerators and denominators. Simply cross-multiply, yielding \( \frac{15}{8} \). This technique proves especially useful in solving equations quickly.

Working with Algebraic Fractions

For algebraic fractions, incorporating reciprocals can simplify expressions like \( \frac{x}{y} \div \frac{a}{b} \). Rewrite it using the reciprocal of the second fraction: \( \frac{x}{y} \times \frac{b}{a} = \frac{xb}{ya} \). Such transformations can make it easier to combine fractions or manipulate equations without tedious calculations.

Visualizing Reciprocals: Graphical Representations

To visualize reciprocals effectively, plot the function \( y = \frac{1}{x} \) on a Cartesian plane. This hyperbolic curve exhibits key characteristics: it approaches the axes but never touches them, creating asymptotes at the x-axis and y-axis.

Key Features of the Reciprocal Graph

The graph consists of two branches. The first is in the first quadrant, where both \( x \) and \( y \) are positive. The second branch lies in the third quadrant, with both values being negative. As \( x \) increases, \( y \) decreases, illustrating their inverse relationship. For instance, at \( x = 1 \), \( y = 1 \); at \( x = 2 \), \( y = 0.5 \); and at \( x = -1 \), \( y = -1 \).

Understanding Asymptotic Behavior

The asymptotic nature of the graph emphasizes the concept of reciprocals. As \( x \) approaches zero from the positive side, \( y \) tends towards infinity. Conversely, as \( x \) approaches zero from the negative side, \( y \) again trends toward negative infinity. This behavior highlights the reciprocal’s unique qualities, making understanding and teaching these concepts more engaging.

Using graphing software can enhance this visual experience. Interactive tools allow users to manipulate values and immediately see the changes on the graph, deepening comprehension of reciprocals and their properties.